第Ⅰ卷 (选择题)
一、选择题
(1)设全 集
集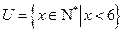 ,集合
,集合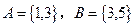 ,则
,则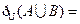 ( )
( )
(A)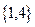 (B)
(B)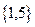 (C)
(C)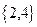 (D)
(D)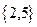
【答案】C
【命题意图】本题考查求集合的并集和补集,集合的子交并补等基本运算是历年高考的热点,属于基础题型,需要考生熟练掌握.
【解析】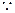
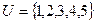 ,
,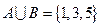 ,
,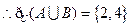 ,或者由狄莫弗性质:
,或者由狄莫弗性质: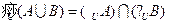 ,故选C.
,故选C.
(2)不等式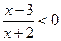 的解集为( )
的解集为( )
(A)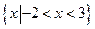 (B)
(B)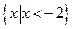
(C)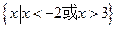 (D)
(D)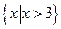
【答案】A
【命题意图】本题考查分式不等式的解法,转化成整式二次不等式求解,蕴涵了等价转化的数学思想.
【解析】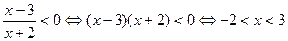 ,故选A.
,故选A.
(3)已知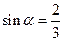 ,则
,则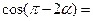
(A)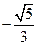 (B)
(B)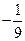 (C)
(C)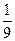 (D)
(D)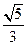
【答案】B
【命题意图】本题考查诱导公式和二倍角的余弦公式,在三角化简求值等运算中,公式是基础.
【解析】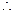
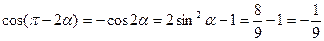 ,故选B.
,故选B.
(4)函数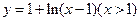 的反函数是
的反函数是
(A)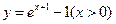 (B)
(B)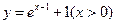
(C)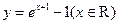 (D)
(D)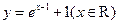
【答案】D
【命题意图】本题考查求函数的反函数的三步骤:1.求原函数的值域,2.反解解析式,3.对调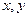 ,写出定义域(即原函数值域).
,写出定义域(即原函数值域).
【解析】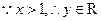 ,由
,由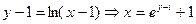 ,
,
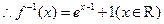 ,故选D.
,故选D.
(5)若变量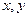 满足约束条件
满足约束条件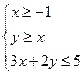 ,则
,则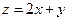 的最大值为
的最大值为
(A)1 (B)2 (C)3 (D)4
(6)如果等差数列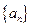 中,
中,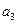 +
+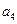 +
+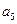 =12,那么
=12,那么 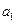 +
+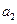 +…+
+…+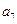 =
=
(A)14 (B)21 (C )28 (D)35
)28 (D)35
【答案】C
【命题意图】本题考查等差数列基本量的计算,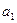 ,
,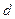 ,
,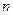 ,
,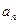 ,
,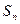 五个量知三求二,应用到方程思想,同时也考查了等差数列的通项公式和前
五个量知三求二,应用到方程思想,同时也考查了等差数列的通项公式和前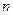 项和公式.
项和公式.
【解析】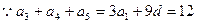 ,
,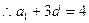 ,而
,而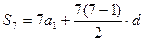
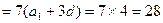 ,故选C.
,故选C.
(7)若曲线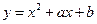 在点
在点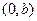 处的切线方程是
处的切线方程是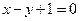 ,则
,则
(A)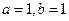 (B)
(B)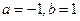
(C)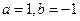 (D)
(D)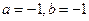
【答案】A
【命题意图】本题考查导函数的几何意义,函数在某点的导函数值等于图象在这点的切线的斜率.
【解析】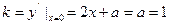 ,又切线过该点
,又切线过该点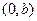 ,
,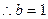 ,故选A.
,故选A.
(8)已知三棱锥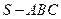 中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成角的正弦值
中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成角的正弦值 为
为
(A)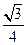 (B)
(B)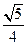 (C)
(C)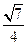 (D)
(D)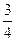

(9)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的放法共有
(A)12种 (B)18种 (C)36种 (D)54种
【答案】B
【命题意图】本题考查排列组合的分配问题,解决方法是:先分组,后全排;也考查了平均分组问题,用除法处理,考生要注意除法意义上的理解.
【解析】先将1,2分为一组,再将3,4,5, 6平均分为2组,共有
6平均分为2组,共有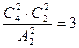 种分法,然后在将三组卡片全排列在3个信封里,不同的放法有
种分法,然后在将三组卡片全排列在3个信封里,不同的放法有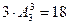 种.故选B.
种.故选B.
(10)△ABC中,点D在边AB上,CD平分∠ACB,若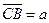 ,
,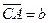 ,
,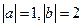 ,则
,则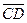 =
=
(A)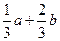 (B)
(B)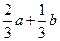 (C)
(C)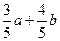 (D)
(D) 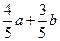
【答案】B
【命题意图】本题考查平面向量加减运算法则和线性基底表示,属于向量基本集合性质;还考查了角平分线定理,这个知识点初高中教材中均未明确提出,很多学生比较生疏,需引起注意.
【解析】由角平分线定理知: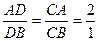 ,
,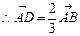
 ,
,
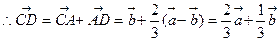 .故选B.
.故选B.
(11)与正方体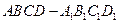 的三条棱
的三条棱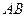 、
、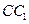 、
、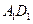 所在直线的距离相等的点
所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个

(12)已知椭圆C: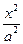 +
+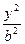 =1
=1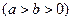 的离心率为
的离心率为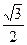 ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若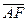 =3
=3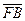 ,则k=
,则k=
(A)1 (B)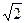 (C)
(C)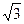 (D)2
(D)2
【答案】B
【命题意图】本题考查直线和圆锥曲线的位置关系,是近年来高考中常考题型,知识覆盖宽,对分解决析问题能力和计算能力要求较高.涉及交点问题,面积问题,夹角问题,弦长问题通常需要联立直线和曲线方程,利用韦达定理求解.本题对椭圆的形状可特殊化处理,简化计算,降低难度.
【解析】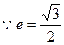 ,
, 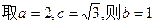 ,
,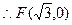 ,椭圆方程为:
,椭圆方程为: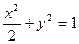
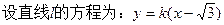 ,联立化简得:
,联立化简得: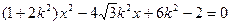 ,
,
设交点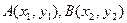 ,由
,由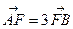 得:
得: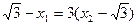 ,代入韦达定理:
,代入韦达定理:
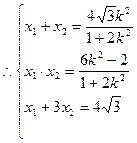 消去
消去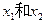 ,解得:
,解得: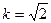 .故选B.
.故选B.
第Ⅱ卷(非选择题)
二.填空题:本大题共4小题,每小题5分,共20分。
(13)已知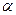 是第二象限的角,
是第二象限的角,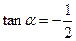 ,则
,则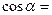 ___________.
___________.
【答案】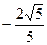
【命题意图】本题考查同角三角函数的基本关系,以及二象限内函数符号.
【解析】由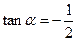 易知:
易知: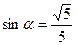 ,
,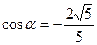 .
.
(14) 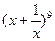 的展开式中
的展开式中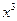 的系数是__________
的系数是__________
【答案】84
【命题意图】本题考查二项式展开式指定某项的系数,关键是由通项公式求出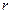 .
.
【解析】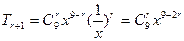 ,令
,令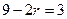 得
得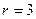 ,故系数为
,故系数为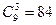 .
.
(15) 已知抛物线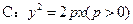 的准线为
的准线为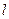 ,过M(1,0)且斜
,过M(1,0)且斜 率为
率为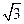 的直线与
的直线与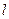 相交于点A,与C的一个交点为B,若
相交于点A,与C的一个交点为B,若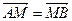 ,则
,则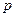 =_________.
=_________.
【答案】2
【命题意图】本题考查直线和抛物线的位置关系,由已知可以直接写出该直线方程,进而求出A点坐标,注意到M为线段AB中点,可得点B的坐标,代入抛物线C即可.
【解析】直线方程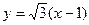 ,令
,令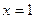 ,得
,得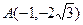 ,而中点
,而中点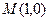 ,所以
,所以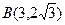 ,代入
,代入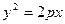 ,解得
,解得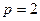 .
.
(16)已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,若OM=ON=3,则两圆圆心的距离MN=________________.
【答案】3
【命题意图】本题考查球体中距离,夹角,可转化到直角三角形中利用垂径定理解决.欲求MN长度,关键找夹角MON.
【解析】设AB中点为P,连接OP,在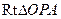 中,
中,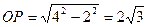 ,
,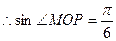 ,
,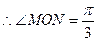 ,则
,则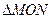 为等边三角形,所以MN=OM=ON=3.
为等边三角形,所以MN=OM=ON=3.











